Delbrin Ahmed – Some large numbers of subuniverses of latices and semilattices

Szeged University, Bolyai Institute
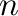
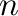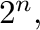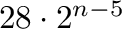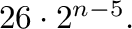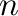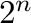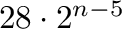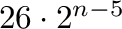We prove that the first largest number of subuniverses of an $n$-element semilattice is $2^n,$ while the second largest number is $28 \cdot 2^{n-5}$ and the third one is $26\cdot 2^{n-5}.$ Also, we describe the $n$-element semilattices with exactly $2^n$, $28 \cdot 2^{n-5}$ or $26\cdot 2^{n-5}$ subuniverses. Moreover, we prove that the fourth largest number of subuniverses of an 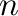$n$-element lattice is 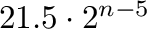$21.5\cdot 2^{n-5}$, and the fifth largest number is 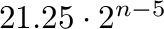$21.25\cdot 2^{n-5}$. 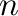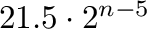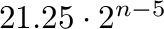Also, we describe the $n$-element lattices with exactly $21.5\cdot 2^{n-5}$ and $21.25\cdot 2^{n-5}$ subuniverses.