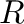
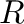 be a commutative ring with identity
be a commutative ring with identity 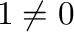 . Zero-divisor graph of
. Zero-divisor graph of 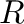 is a graph with vertex set as non-zero zero-divisors of
is a graph with vertex set as non-zero zero-divisors of 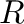 such that distinct vertices
such that distinct vertices 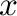 and
and 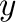 are adjacent if
are adjacent if 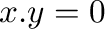 .
.
Consider the rings
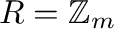 and
and
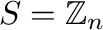 ,
, 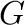 and
and 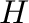 their zero-divisor graphs respectively with
their zero-divisor graphs respectively with
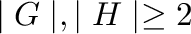 . We discuss the diameter and girth of tensor product and lexicographic product of
. We discuss the diameter and girth of tensor product and lexicographic product of 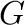 and
and 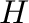 .
.
This is joint work with Pradeep Singh.