Insa Cremer – Strong semilattice decomposition of m-domain rings

University of Latvia
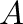
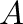A semigroup $A$ is said to be a D-semigroup if there exists some subset 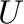$U $ of its set of idempotents 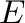$E $ such that, for every 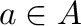$a\in A $, there exists the smallest 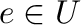$e\in U $ in the sense of the usual partial order of idempotents with the property that 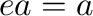$ea=a $. So on every D-semigroup, we can define a unary operation assigning to each 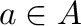$a\in A $ the smallest idempotent 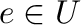$e\in U $ with $ea=a $.

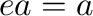An m-domain ring is a ring 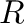$R$ such that, for every element 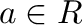$a\in R $, there exists a central idempotent 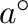$a^{\circ} $ such that 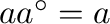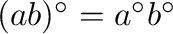$aa^{\circ}=a $, $(ab)^{\circ} = a^{\circ}b^{\circ} $ and, if 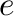$e $ is an idempotent such that 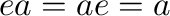$ea=ae=a $, then 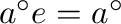$a^{\circ}e=a^{\circ} $. The multiplicative semigroup of an m-domain ring is a D-semigroup (with the unary operation $^{\circ} $).

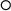Given an m-domain ring 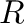$R$, we can decompose it into an inverse system of pairwise disjoint right-cancellative D-semigroups with identities over the set of idempotent elements of 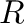$R$. In the talk, the following results on this decomposition will be presented.

First, the strong semilattice of D-semigroups obtained from this inverse system is the multiplicative D-semigroup of the ring 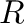$R$.

Second, let 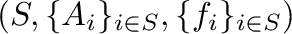$(S, \{A_{i}\}_{i\in S}, \{f_{i}\}_{i\in S} ) $ be an inverse system of pairwise disjoint right-cancellative D-semigroups with identities 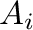$A_{i} $ over some lower semilattice 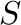$S$. 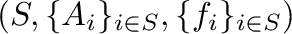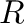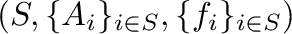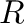If the strong semilattice of D-semigroups obtained from the inverse system $(S, \{A_{i}\}_{i\in S}, \{f_{i}\}_{i\in S} ) $ is the multiplicative D-semigroup of some m-domain ring $R$, then the inverse system $(S, \{A_{i}\}_{i\in S}, \{f_{i}\}_{i\in S} ) $ is the decomosition of the m-domain ring $R$.