Stefano Fioravanti – Expansions of abelian squarefree groups

Johannes Kepler University Linz

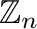
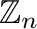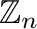We investigate finitary functions from $\mathbb{Z}_{n}$ to $\mathbb{Z}_{n}$ for a squarefree number $n$

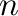. We show that the lattice of all clones on the squarefree set 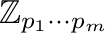$\mathbb{Z}_{p_1\cdots p_m}$ which contain the addition of 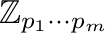$\mathbb{Z}_{p_1\cdots p_m}$ is finite. We provide an upper bound for the cardinality of this lattice through an injective function to the direct product of the lattices of all 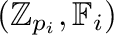$({\mathbb{Z}}_{p_i}, {\mathbb{F}}_i)$ -linearly closed clonoids, 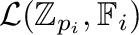$\mathcal{L}({\mathbb{Z}}_{p_i}, {\mathbb{F}}_i)$ , to the $p_i+1$

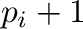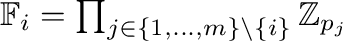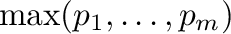power, where ${\mathbb{F}}_i = \prod_{j \in \{1,\dots,m\}\backslash \{i\}}{\mathbb{Z}}_{p_j}$ . Furthermore, we prove that these clones can be generated by a set of functions of arity at most $\max(p_1,\dots,p_m)$ .