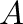
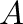, the congruence lattices
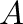of all algebras defined on ordered by inclusion form a finite lattice
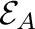; the
problem is to characterize those finite lattices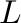 
which can be represented in the
form
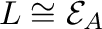for some set 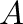. This means that the properties of the lattice
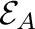has to be determined. We will present an overview of some known properties, and also of some open problems.
Since the join- and meet-irreducible elements of a finite lattice are its "building-stones", an important objective
is to describe these elements in
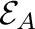. The join-irreducible elements of
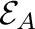have been completely characterized, while he problem on meet-irreducible elements of
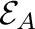has several, but only partial results.