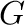 . In several cases, including symmetric terms of arity
. In several cases, including symmetric terms of arity 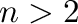 (so
(so 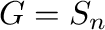 is the symmetric group) the local-to-global approach fails.
is the symmetric group) the local-to-global approach fails.
In this talk, I would like to discuss the local-to-global approach for terms, whose variables are invariant under permutations from a given permutation group 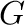 . In several cases, including symmetric terms of arity
. In several cases, including symmetric terms of arity 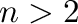 (so
(so 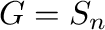 is the symmetric group) the local-to-global approach fails.
is the symmetric group) the local-to-global approach fails.
This is joint work with Alexandr Kazda.