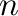
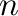 -ary operations which are called cyclic and weak
near-unanimity using the concepts of cyclic and weak near-unanimity terms in the study of universal algebra, respectively. The Menger algebras of these two
-ary operations which are called cyclic and weak
near-unanimity using the concepts of cyclic and weak near-unanimity terms in the study of universal algebra, respectively. The Menger algebras of these two 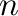 -ary operations defined on a fixed set are constructed and some algebraic properties are investigated. In particular, we
provide the necessary and sufficient conditions under which an abstract Menger algebra can be isomorphically represented by such
-ary operations defined on a fixed set are constructed and some algebraic properties are investigated. In particular, we
provide the necessary and sufficient conditions under which an abstract Menger algebra can be isomorphically represented by such 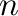 -ary operations.
-ary operations.