Agata Pilitowska – Semilattice ordered algebras with constants

Warsaw University of Technology, Warsaw, Poland
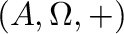
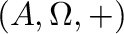A semilattice ordered algebra is an algebra of the form $(A,\Omega,+)$, where 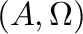$(A,\Omega)$ is an algebra of a given type, 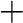$+$ is a join-semilattice operation, and operations from the set 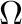$\Omega$ distribute over the operation 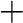$+$. Important examples of ordered algebras are given not only by Boolean algebras, Heyting algebras, lattice-ordered groups, MV-algebras but also by widely investigated quantales or well known additively idempotent semirings.

The basic role in the theory is played by extended power algebras of non-empty subsets and extended algebras of (non-empty) subalgebras. The aim of the present talk is to describe the properties of semilattice ordered algebra with constants, i.e. with operations of the arity equal to zero (or in the case of power constructions with the empty subset and the empty subalgebra).

This is joint work with Anna Zamojska-Dzienio.