Miroslav Ploscica – Congruence lattices of Abelian l-groups

Safarik's University Kosice, Slovakia
We consider the problem of describing the lattices of compact $\ell$-ideals of Abelian lattice-ordered groups. (Equivalently, describing the congruence lattices of Abelian lattice-ordered groups.) It is known that these lattices have countably based differences and admit a Cevian operation. 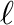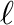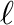Our first result says that these two properties are not sufficient: there are lattices having both countably based differences and Cevian operations, which are not representable by compact $\ell$-ideals of Abelian lattice-ordered groups. As our second result, we prove that every completely normal distributive lattice of cardinality at most 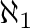$\aleph_1$ admits a Cevian operation. This complements the recent result of F. Wehrung, who constructed a completely normal distributive lattice without a Cevian operation of cardinality 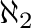$\aleph_2$.