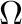
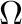 some variety
some variety 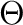 . We denote by
. We denote by
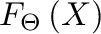 the free
algebra of this variety generated by the set of free generators
the free
algebra of this variety generated by the set of free generators 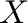 . We
consider only finitely generated free algebras. We denote by
. We
consider only finitely generated free algebras. We denote by
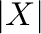 the quantity of the elements of the set
the quantity of the elements of the set 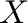 .
.
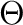 is an IBN-variety (or variety
which has an IBN propriety), if from
is an IBN-variety (or variety
which has an IBN propriety), if from
 we can conclude that
we can conclude that
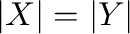 .
.
The concept of variety with IBN (invariant basic number) propriety first
appeared in ring theory. It is known that if we consider some field 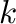 , the
vector space
, the
vector space 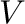 over this field such that
over this field such that
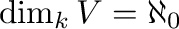 ring
ring 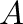 of all linear operators on this vector space (
of all linear operators on this vector space (
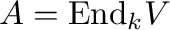 ), then
), then
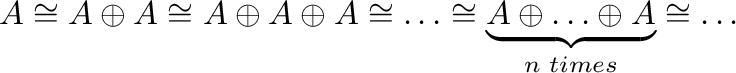 , i.e., the
variety
, i.e., the
variety
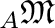 of all rights modules over the ring
of all rights modules over the ring 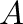 has not
the IBN propriety.
has not
the IBN propriety.
The proving of the IBN propriety of some variety is very important in universal algebraic geometry. This is a milestone in the study of the relation between geometric and automorphic equivalences of algebras of this variety.
We will look at some examples where the IBN property of certain varieties
can be proved directly. For example for every signature 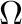 the
variety defined by the empty set of identities has the IBN property.
the
variety defined by the empty set of identities has the IBN property.
We will discuss very simple but very useful
 some varieties of universal algebras of a signature
some varieties of universal algebras of a signature 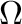 ,
,
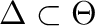 and
and 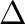 is an IBN-variety then
is an IBN-variety then 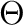 is also an IBN-variety.
is also an IBN-variety.We will consider applications of this theorem.
We will consider many-sorted universal algebras as well as one-sorted. So all concepts and all results will by generalized for the many-sorted case.