Oleg Gutik – On the monoid of cofinite partinal isometries of positive integers

Lviv National University

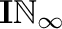
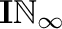We discussed on the monoid $\mathbf{I}\mathbb{N}_{\infty}$ of all partial cofinite isometries of positive integers with the usual metric. We describe the structure of 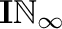$\mathbf{I}\mathbb{N}_{\infty}$ and describe all homomorphisms frov 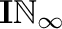$\mathbf{I}\mathbb{N}_{\infty}$ into the monoid 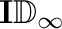$\mathbf{I}\mathbb{D}_{\infty}$ of all partial cofinite isometries of integers with the usual metric. Also we show that 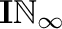$\mathbf{I}\mathbb{N}_{\infty}$ is not finitely generated, and moreover the monoid 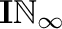$\mathbf{I}\mathbb{N}_{\infty}$ does not contain a minimal generating set.

This is a join work with Anatolii Savchuk.