
 is said to be a D-semigroup if there exists
some subset
is said to be a D-semigroup if there exists
some subset  of its set of idempotents
of its set of idempotents  such that, for every
such that, for every  , there exists the smallest
, there exists the smallest  in the sense of the usual partial order of idempotents with the property that
in the sense of the usual partial order of idempotents with the property that  . So on every D-semigroup, we can define a unary operation assigning to each
. So on every D-semigroup, we can define a unary operation assigning to each  the smallest idempotent
the smallest idempotent  with
with  .
.
An m-domain ring is a ring 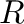 such that, for every element
such that, for every element  , there exists a central idempotent
, there exists a central idempotent  such that
such that
 ,
,
 and, if
and, if  is an idempotent such that
is an idempotent such that  , then
, then
 . The multiplicative semigroup of an m-domain ring is a D-semigroup (with the unary operation
. The multiplicative semigroup of an m-domain ring is a D-semigroup (with the unary operation  ).
).
Given an m-domain ring 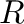 , we can decompose it into an inverse system of pairwise disjoint right-cancellative D-semigroups with identities over the set of idempotent elements of
, we can decompose it into an inverse system of pairwise disjoint right-cancellative D-semigroups with identities over the set of idempotent elements of 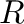 . In the talk, the following results on this decomposition will be presented.
. In the talk, the following results on this decomposition will be presented.
First, the strong semilattice of D-semigroups obtained from this inverse system is the multiplicative D-semigroup of the ring 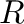 .
.
Second, let
 be an inverse system of pairwise disjoint right-cancellative D-semigroups with identities
be an inverse system of pairwise disjoint right-cancellative D-semigroups with identities  over some lower semilattice
over some lower semilattice  . If the strong semilattice of D-semigroups obtained from the inverse system
. If the strong semilattice of D-semigroups obtained from the inverse system
 is the multiplicative D-semigroup of some m-domain ring
is the multiplicative D-semigroup of some m-domain ring 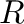 , then the inverse system
, then the inverse system
 is the decomosition of the m-domain ring
is the decomosition of the m-domain ring 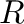 .
.