
 , for
, for
 , was introduced. A natural duality for the variety
, was introduced. A natural duality for the variety  generated by
generated by  was presented. The objects of the dual category
was presented. The objects of the dual category  are multi-sorted topological structures. In this talk we give a description and an axiomatisation of the dual category
are multi-sorted topological structures. In this talk we give a description and an axiomatisation of the dual category  . We moreover claim that the category
. We moreover claim that the category  is isomorphic to a category
is isomorphic to a category  of single-sorted topological structures. The objects of
of single-sorted topological structures. The objects of  are Priestley spaces endowed with a continuous retraction in which the order has a natural ranking. As a nice application we show that the size of the free algebra
are Priestley spaces endowed with a continuous retraction in which the order has a natural ranking. As a nice application we show that the size of the free algebra
 is given by a polynomial in
is given by a polynomial in 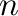 of degree six.
of degree six.
This is joint work with Brian A. Davey and Andrew P.K. Craig