Anatolii V. Zhuchok – The least dimonoid congruence on the free
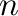 -nilpotent
-nilpotent 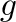 -dimonoid
-dimonoid
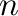 -nilpotent
-nilpotent 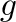 -dimonoid
-dimonoid
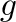 -dimonoids [2] are a generalization of dimonoids [1] while every 0-dialgebra with associative operations [3] is a linear analog of a
-dimonoids [2] are a generalization of dimonoids [1] while every 0-dialgebra with associative operations [3] is a linear analog of a 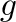 -dimonoid. Free
-dimonoid. Free 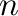 -nilpotent
-nilpotent 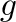 -dimonoids were constructed in [4].
-dimonoids were constructed in [4].
Let 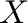 be an arbitrary nonempty set, and let
be an arbitrary nonempty set, and let 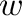 be an arbitrary
word over
be an arbitrary
word over 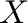 . For every
. For every 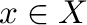 , the number of occurrences of the element
, the number of occurrences of the element 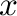 in
in 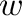 is denoted by
is denoted by 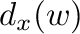 . If
. If 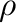 is a congruence on a
is a congruence on a 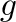 -dimonoid
-dimonoid
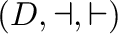 such that
such that
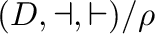 is a dimonoid, we say that
is a dimonoid, we say that 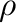 is a dimonoid congruence. If
is a dimonoid congruence. If 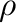 is a congruence on a
is a congruence on a 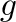 -dimonoid
-dimonoid
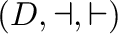 such that operations of
such that operations of
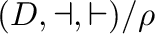 coincide, we say that
coincide, we say that 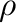 is a semigroup congruence.
is a semigroup congruence.
Theorem. Let 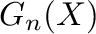 be the free
be the free 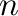 -nilpotent
-nilpotent 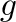 -dimonoid,
-dimonoid,
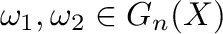 .
.
(i) Define a relation
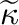 on
on 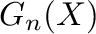 by
by
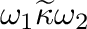 if and only if one of the following conditions holds:
if and only if one of the following conditions holds:
(1)
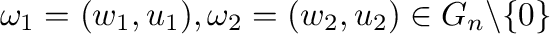 and
and
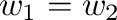 ,
,
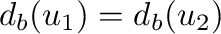 ;
;
(2)
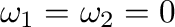 .
.
Then
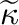 is the least dimonoid congruence on
is the least dimonoid congruence on 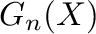 .
.
(ii) Define a relation
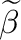 on
on 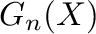 by
by
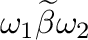 if and only if one of the following conditions holds:
if and only if one of the following conditions holds:
(1)
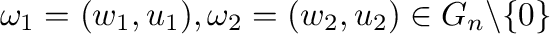 and
and
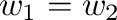 ;
;
(2)
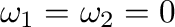 .
.
Then
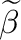 is the least semigroup congruence on
is the least semigroup congruence on 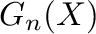 .
.
References
 -dimonoids.
Algebra Discrete Math. 18, no. 1, 138–148 (2014)
-dimonoids.
Algebra Discrete Math. 18, no. 1, 138–148 (2014)